Smoothing

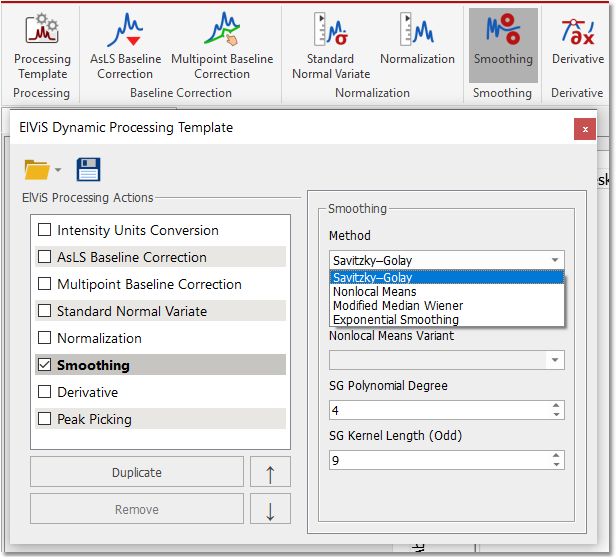
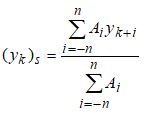频谱的信噪比（S/N）可以通过平滑（或滤波）技术得到增强。噪声包含信号的高频（与波谱特征相比）波动。平滑技术对波谱数据进行低通滤波器处理，以去除噪声，同时保留信息丰富的波谱信号。

Mnova ElViS 采用了一些最常用的信号平滑算法。

您可以从方法下拉列表中选择所需的平滑算法：非局部均值算法、修正中值维纳算法、指数平滑算法和萨维茨基-戈莱算法。

萨维茨基-戈莱算法"：这种方法将一组连续数据点与多项式进行最小二乘拟合，并将计算出的拟合多项式曲线的中心点作为新的平滑数据点。

Savitzky 和 Golay 证明，可以得出一组整数（A-n、A-(n-1)......、An-1、An），并将其用作加权系数来执行平滑操作。使用这些加权系数（称为卷积整数），结果完全等同于用多项式拟合数据，如前所述，而且在计算上更有效，速度更快。因此，萨维茨基-戈莱算法的平滑数据点 (yk)s 由下式给出：

用卷积整数集代替平滑信号，可以直接得到其 1 阶、2 阶......、m 阶导数，因此萨维茨基-戈莱算法对于计算由离散点和等距点组成的噪声信号的导数非常有用。